Mathematical Definition:

PCA is similar to Factor Analysis, in that will we decompose your data into a set of components that maximise variance in your data.

Ok, let's take a step back. It's simple to make an average of a set templates, for each point in the template you take the sum of the x coordinates (horizontal) and divide by the number of templates, you do the same for the y coordinates (vertical). The resulting point is roughly in the middle of the original positions in all the templates. Its exact position is called the centre of gravity, in the it is biased to locations with high point density. So, now you have an average, and it still looks like a face, if it doesn't you're doing it wrong and should look at this tutorial.

Example of an average template.

It is possible to describe a face in your dataset as the amount by which that face deviates from the average. For each point in the face's template we subtract (separately, in both x and y coordinates) the coordinates of the corresponding point in the average template. We now have the deviation of each point from the average, this is useful as we could, for example, work out how 'unusual' a face is. The more a face deviates from the average, the more 'unusual' it is. These measure have been shown to be linked to perceptions of attractiveness and familiarity (amongst many others).

But on their own these deviations are not particularly useful, they are absolute deviations, in pixel space, they tell use little about the nature of the these deviations. It would be useful to know what sorts of changes are most common throughout the data-set. For this, we have PCA.

PCA, looks at the deviations from the average and finds the changes that are most prevalent in the data-set, i.e. explain the most variance. These changes are described as a linear transform, i.e. for each template point, the point is shifted in a fixed direction, only the amount of shift applied is changed. The transform could make the face longer and thinner, by shifting all the points vertically away from the centre and horizontally towards it. Another transform could make the chin larger and more prominent, but leave the rest of the face along. Both combined would make for a thin face with a big chin. The amounts of each transform are called the parameters and the transform itself is referred to as a component.

To recap, a face in a PCA model is described as a weighted sum of the PCA components, plus the average face template.

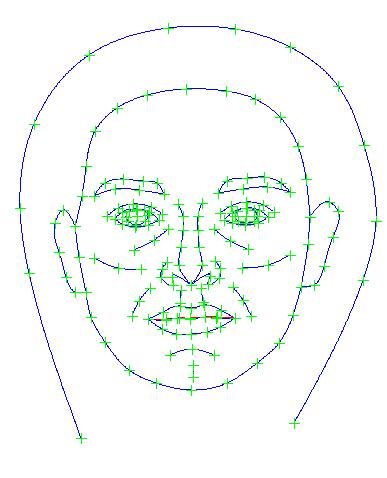
Example of face shape PCA using Psychomorph templates
	+		+		+		+

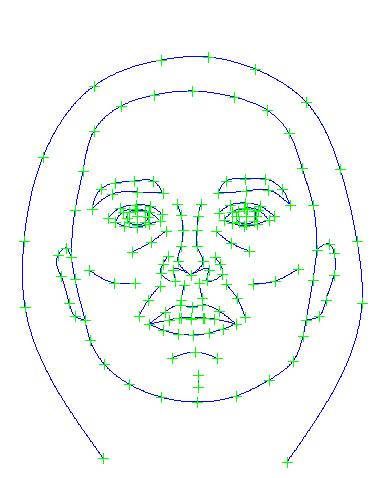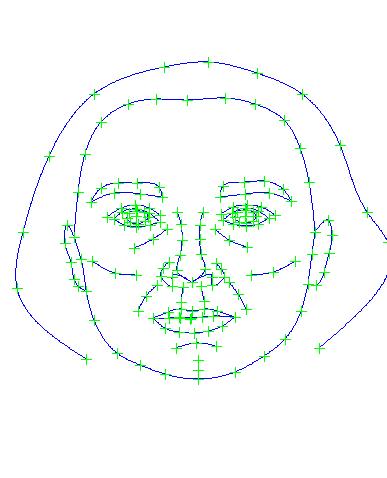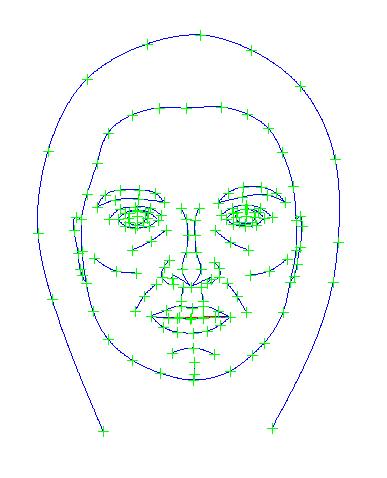Average

First Component

Second Component

Third Component

Fourth Component

PCA models can be built using Psychomorph’s ASM and PCI functions. ASM (Active Shape Model) applies PCA to templates as explained above. PCI (Principal Component Images) applies PCA to the pixels of an image set.